Monthly Archives: June 2013
Fast Path Finding (part II)
Harder, Better, Faster, Stronger
Last week we had a first look at a simple path finding algorithm with application to games. This week, let us have a look a the relative performance of the implementations considered: C# with a naïve implementation that scans the whole map multiple times; a C# implementation that uses lists to maintain and visit only the border of the solved region (affording massive speed-ups, one hopes); and C++ versions of these two variants, plus a C++ variant that uses set (as bitmaps) to maintain the border list.
In any quantitative study, the first thing to do is to collect data. The best way is to automate the collection, by, for example, adding a function that puts the player in all legal positions on the map, compute all the shortest paths, and measures how long it takes. One may also consider disabling the on-demand power policy as the CPU may jump…
View original post 551 more words
Merge Sort
C++ Code To Illustrate Merge-Sort In A Single Array:
#include<iostream.h>
void merge(int A[],int p, int q, int r)
{
int i,j,k;
int x = q-p+1;
int y = r-q;
int B[20];
int C[20];
B[x] = 10000;
C[y] = 10000;
for (i=0;i<x;i++) B[i] = A[p+i];
for (i=0;i<y;i++) C[i] = A[q+i+1];
i=0;j=0;
for (k=p;k<=r;k++)
{
if (B[i]<=C[j]) A[k] = B[i++];
else A[k] = C[j++];
}
}
void mergesort(int A[], int p,int r)
{
int q;
if (p<r)
{
q = (p+r)/2;
mergesort(A,p,q);
mergesort(A,q+1,r);
merge(A,p,q,r);
}
}
void main()
{
int A[20],n;
cout << “Enter Length Of Array \n” ;
cin >> n;
cout << “Enter Array \n”;
int i;
for (i=0;i<n;i++) cin >> A[i];
mergesort(A,0,n-1);
cout << “Sorted Array \n” ;
for (i=0;i<n;i++) cout << A[i] << ” “;
}
Heapsort
Java Code To Illustrate Heapsort:
package heapsort;
import edu.princeton.cs.introcs.*;
public class Heapsort
{
public static int heapsize;
public static int Parent(int i)
{
return i/2;
}
public static int Left(int i)
{
return 2*i+1;
}
public static int Right(int i)
{
return 2*i+2;
}
public static void MaxHeapify(int A[], int i)
{
int l = Left(i);
int r = Right(i);
int greatest,temp;
if (l<heapsize && A[l]>=A[i]) greatest = l;
else greatest = i;
if (r<heapsize && A[r]>=A[greatest]) greatest = r;
if (greatest!=i)
{
temp = A[greatest];
A[greatest] = A[i];
A[i] = temp;
MaxHeapify(A,greatest);
}
}
public static void BuildHeap(int A[], int n)
{
int i;
for (i=(n/2)-1;i>=0;i–) MaxHeapify(A,i);
}
public static void heapsort(int A[])
{
BuildHeap(A,heapsize);
int i,temp;
for (i=A.length-1;i>=1;i–)
{
temp = A[0];
A[0] = A[i];
A[i] = temp;
heapsize–;
BuildHeap(A,heapsize);
}
}
public static void displayheap(int A[])
{
int height = (int)((Math.log10(A.length)) / (Math.log10(2)));
int spaces =…
View original post 82 more words
Quick: How Does Quicksort Work?
Every now and then, we need to remember how some complex algorithm works. For some, code works well. Or puzzles. Others prefer an explanation with examples. A third group likes to see what is going on.
The AlgoViz.org portal contains visualizations of all kinds of algorithms for the visually inclined.
Algorithms: Why are they useful?
This is such a hilarious question I just had to take a crack at it.
First, let’s get one thing out of the way: even single-line procedures are technically algorithms. Hence,
1 | Jeffrey. Love me. |
is an algorithm, provided by Maude to The Dude. Admittedly, however, those are not very interesting algorithms (though they can be plenty useful), so let’s focus on more elaborate ones.
Take, for example, lovemaking. You have an algorithm for that.
It has bifurcations.
1 2 3 4 | If He moans Then Move to Next Step. |
It has loops.
1 2 3 4 5 6 | Repeat Forwards. Delay 0.1s Backwards. Delay 0.2s Until (something magical happens) or (you're exhausted). |
It has subroutines.
1 2 3 4 | Do That Thing That Always Sends Him To The Moon. Do Cuddle. |
It relies heavily on random number generators.
1 2 3… |
View original post 169 more words
QuickSort
Java Code To Illustrate QuickSort:
package quicksort;
import edu.princeton.cs.introcs.*;
public class QuickSort
{
public static void display(int a[])
{
for (int k=0;k<a.length;k++) System.out.print(a[k] + ” “);
System.out.println();
}
public static int Partition(int A[], int p, int r)
{
int pivot = A[r];
int i = p-1;
int temp;
for (int j=p;j<r;j++)
{
if (A[j]<=pivot)
{
i++;
temp = A[i];
A[i] = A[j];
A[j] = temp;
}
}
temp = A[r];
A[r] = A[i+1];
A[i+1] = temp;
return i+1;
}
public static int HoarePartition(int A[], int p, int r)
{
int i = p;
int j = r;
int x = A[p];
int temp;
while (i<j)
{
while(A[j]>=x && j>p) –j;
while(A[i]<=x && i<r) ++i;
if(i<j)
{
temp = A[i];
A[i] = A[j];
A[j] = temp;
}
}
temp = A[p];
A[p] = A[j];
A[j] = temp;
return j;
}
public static void quicksort(int A[],int p, int r)
{
if…
View original post 55 more words
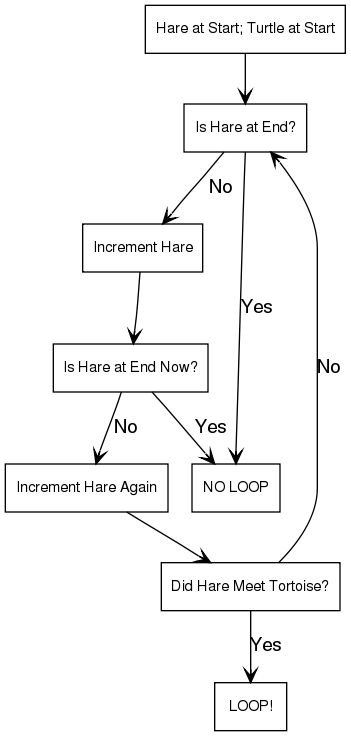
Loop detection in Singly Linked List.
Floyd’s Cycle Detection Algorithm (The Tortoise and the Hare) :
In Brief : How do you determine if your singly-linked list has a cycle?
In the late 1960s, Robert W. Floyd invented an algorithm that worked in linear (O(N)) time. It is also called Floyd’s cycle detection algorithm or The Tortoise and the Hare
The easiest solution to the cycle detection problem is to run through the list, keeping track of which nodes you visit, and on each node check to see if it is the same as any of the previous nodes. It’s pretty obvious that this runs in quadratic (O(N^2)) time… not very efficient, and actually more complicated than this one.
The Tortoise and the Hare is possibly the most famous cycle detection algorithm, and is surprisingly straightforward. The Tortoise and the Hare are both pointers, and both start at the top of the list. For each iteration…
View original post 105 more words
Graph matching & Levenshtein distance (p1)
Graphs are mathematical structures widely used to abstract and model relation dynamics in various systems. For example, the web can be represented by a graph in which nodes (vertices) correspond to webpages and edges (links) correspond to hyperlinks.
Definition: A graph $latex G$ is a set of vertex $latex V$ connected by edges $latex E$ denoted as the ordered pair $latex G=(V,E)$.
A very important problem in graph theory is called graph matching which is measuring the similarity between graphs. This problem has a variety of applications such as social networks, image processing and bioinformatics.
How do we know if two graphs are the same? Well, you can try to take nodes of one graph and rearrange it to look like the other graph without adding or removing edges. If the two graphs end up looking identical (ignoring labels if any) then we say that the graphs are isomorphic. You can…
View original post 386 more words
Counting Sort
Java Code To Illustrate Counting Sort:
package countingsort;
import java.util.Scanner;
public class CountingSort
{
public static void display(int A[])
{
for (int i=0;i<A.length;i++) System.out.print(A[i] + ” “);
System.out.println();
}
public static void CountingSort(int A[], int n, int k)
{
int i;
int B[] = new int[n];
int C[] = new int[k+1];
for (i=0;i<k+1;i++) C[i] = 0;
display(C);
for (i=0;i<n;i++) C[A[i]]++;
display(C);
for (i=1;i<k+1;i++) C[i] += C[i-1];
display(C);
for (i=A.length-1;i>=0;i–)
{
B[C[A[i]]-1] = A[i];
C[A[i]]–;
}
System.out.println(“Sorted Array:”);
display(B);
}
public static void main(String[] args)
{
Scanner x = new Scanner(System.in);
System.out.println(“Counting Sort”);
System.out.println(“Enter Number Of Elements”);
int n = x.nextInt();
int A[] = new int[n];
int max;
System.out.println(“Enter array”);
for (int i=0;i<n;i++) A[i] = x.nextInt();
max = A[0];
for (int i=0;i<n;i++) if (A[i]>max) max = A[i];
CountingSort(A,n,max);
}
}